本章重点: 简单的论证了即使有Noise,机器依然可以学习,VC Dimension对泛化依然起作用;介绍了一些评价Model效果的Error Measurement方法。
一论证即使有Noisy,VC Dimension依然有效;
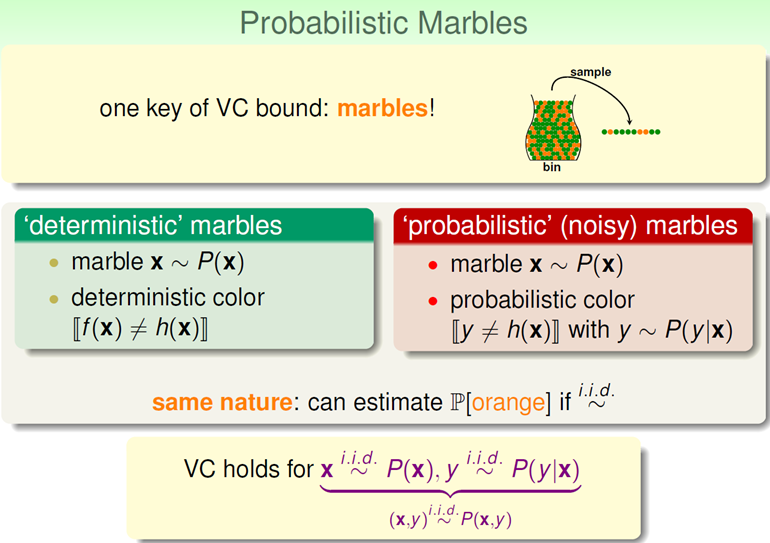
| 下图展示了主要思想,以前的数据集是确定的(Deterministic),现在加了Noisy变成了分布函数了,即对每个一x,y出现的概率是P(y | x)。可以这么理解,概率表示的是对事件确定的程度,以前确定性的数据集是 |
| P(y | x) = 1, for y = f(x) |
| p(y | x) = 0, for y != f(x), |
| 加入了Noisy,便不是了,有一定的概率例如0.7是应该出现的值,0.3则为犯错的概率,即出现了不该出现的值。这便是加入Noisy的模型,只不过增加了概率分布(其实以前也是,只不过是1和0罢了),只要y是p(y | x)取值的,就可以认为以前证明机器可以学习的方法依然奏效,VC Dimension有限即可推断Ein和Eout一致。 |

二关于Error
对于Train完之后的error,有pointwise,out of sample以及classification(0/1)三种。


PointWise error实际上就是按数据集每个点比较并计算平均,像Linear Regression里面的最小平方和的cost function就是这类。即下图所示。

实际上,机器学习的Cost Function即来自于这些error,也就是算法里面的迭代的目标函数,通过优化使得Error(Ein)不断变小。
对于这些error,实际上和使用场景关心很大,我们知道Model的判断结果大致有4种:
TP:Model预测是对的,实际也是对的,这个是好事;
FP:Model预测是对的,但实际是错的,这是坏事,即false accpet;
FN:Model预测是错的,但实际是对的,这个是坏事,即false reject;
TN:Model预测是错的,实际也是错的,这个是好事。
两种错误,FP和FN,这两者在不同情形严重情况不同,所以需要具体情况具体分析。一般错误函数的选择采取下面的策略,Plausible或者Friendly。



